http://www.lydsy.com/JudgeOnline/problem.php?id=2213

题目大意：

在一个无向图中有T条边，每个点至少和两条边相连，每条边有一个长度，询问从给定起点到给定终点的包含N条边的路最短是多长。

问题规模：

1<=N<=1000000000, 1<=T<=100

这题我了解到3个方法，都很神牛，很有启发。

1.基于倍增的floyd

官方的解法。假设我们已经知道了两点间经过k条边的最短路，就可以利用floyd求出两点间经过k*2条边的最短路，于是我们可以依次求出经过1,2,4,8,16...条边的最短路，它们正好可以组成任何二进制数，我们只要把N分解成这些的和，再用floyd求一遍就可以了。复杂度O(T^3 logN)。

2.矩阵乘法思想

看到这题的数据应该很多人想到矩阵乘法快速幂，但矩阵乘法表示的是乘积的和，如果是要求经过N条边的路径数就可以直接这么做了，无奈之下只好放弃了这个想法。但其实我们可以尝试定义一个新的矩阵乘法，使它可以表示我们需要的结果。

原始的矩阵乘法是这样的：如果C=A*B 那么

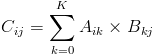
我们可以定义C=A@B

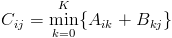
于是样例的结果就可以表示为

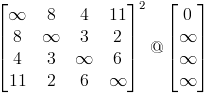
可以证明运算@是满足结合律的，所以也可以用快速幂求出。

这个方法时间复杂度跟floyd是一样的O(T^3 logN)，而且写起来也差不多，以至于我认为它们本质上是一种方法。

3.部分贪心思想

这个是GYH神牛的论文《部分贪心思想在信息学竞赛中的应用》里的，核心有两点：

1.最短路径一定在一条较短边（这条路上的最短边）上来回走了很多次

2.路径上的其他边至多经过两次

证明详见论文。于是我们只需算出起点和终点到每个点经过2*T条边的最短路，然后枚举经过很多次的边，就可以在O(T^2)的时间内解决了。

题解转自http://hi.baidu.com/lilymona/item/3b401d86d22c6fd6d0f8cdf5

代码是写了第二种办法。

#include<cstring>
#include<cstdio>
#include<algorithm>
#include<climits>
#include<cmath>
using namespace std;
const int N=102,M=1005;
int n,e,s,t,vis[M],tot;

struct matrix 
{
	int a[N][N];
	int *operator [](int x) { return a[x];}
	void clear()
	{
		memset(a,63,sizeof(a));
	}
	matrix operator*(matrix b) 
	{
		matrix c;
		memset(c.a,63,sizeof(c.a));
		for(int i=1;i<=tot;++i)
			for(int j=1;j<=tot;++j)
				for(int k=1;k<=tot;++k)
					c[i][j]=min(c[i][j],a[i][k]+b[k][j]);
		return c;
	}
	matrix operator^(int n) 
	{
		matrix b;b=*this;--n;
		while(n) 
		{
			if(n&1) b=b**this;
			*this=*this**this;
			n/=2;
		}
		return b;
	}
}a;

int get(int x)
{
	if(!vis[x])	vis[x]=++tot;
	return vis[x];
}

int main()
{
	scanf("%d%d%d%d",&n,&t,&s,&e);
	a.clear();
	memset(vis,0,sizeof(vis));tot=0;
	for(int i=0;i<t;i++)
	{
		int z,x,y;scanf("%d%d%d",&z,&x,&y);
		x=get(x);y=get(y);
		a[x][y]=a[y][x]=z;
	}
	s=get(s);e=get(e);
	matrix ans=a^n;
	printf("%d\n",ans[s][e]);
}