http://www.lydsy.com/JudgeOnline/problem.php?id=3124

题意

一棵树，求直径和有多少条边一定在直径上。

题解

我就不说我省选有多傻叉了。

首先DFS求出直径，

显然一定在直径上的边一定是任意一条直径上连续的一段。

所以我们遍历求出的直径（红色+蓝色）上的每个点x，

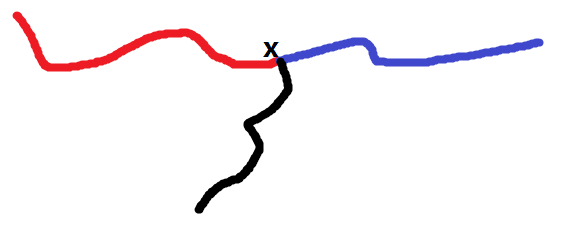
如果以这个点为起点，在不访问直径上的点的情况下，

求出一条最长链，图中的黑色

如果等于蓝色的长度或红色的长度，那么这段蓝色或红色就不是一定在直径上。

这样不断缩小左右端点，剩下的链上的边就是答案

#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=200011,M=N*2;
int v[M],w[M],next[M],head[N],k=1;
long long d[N],dep[N],ans1,tmp;
int n,pre[N],A,B,leaf;bool vis[N];

void add(int x,int y,int z)
{
	v[++k]=y;w[k]=z;next[k]=head[x];head[x]=k;
	v[++k]=x;w[k]=z;next[k]=head[y];head[y]=k;
}

void dfs(int x,int fa)
{
	pre[x]=fa;
	if(dep[x]>tmp)
		tmp=dep[x],leaf=x;
	for(int i=head[x];i;i=next[i])
		if(v[i]!=fa)
			dep[v[i]]=dep[x]+w[i],dfs(v[i],x);
}

void  find(int x,int fa)
{
	tmp=max(tmp,d[x]);
	for(int i=head[x];i;i=next[i])
		if((v[i]!=fa) && (!vis[v[i]]))
			d[v[i]]=d[x]+w[i],find(v[i],x);
}

int main()
{
	scanf("%d",&n);int x,y,z;
	for(int i=1;i<n;i++)
		scanf("%d%d%d",&x,&y,&z),add(x,y,z);
	tmp=dep[1]=0;dfs(1,0);A=leaf;
	tmp=dep[A]=0;dfs(A,0);B=leaf;
	ans1=tmp;
	printf("%lld\n",ans1);
	memset(vis,0,sizeof(vis));
	for(int i=B;i;i=pre[i]) vis[i]=1;
	bool flag=1;int left=A,right=B;
	for(int i=B;i;i=pre[i])
	{
		long long ldist=dep[i],rdist=ans1-dep[i];
		tmp=d[i]=0;find(i,0);
		if((tmp==ldist) && flag) 
			left=i,flag=0;
		if(tmp==rdist) right=i;
	}
	int ans2=0;
	for(int i=right;i!=left;i=pre[i]) ans2++;
	printf("%d\n",ans2);
}